La navigation astronomique a été le seul moyen de positionnement au large jusqu'à l'apparition des systèmes par satellites deuxième moitié du XXe siècle.
5.1 Historique
5.1.1 Astronomie
L'astronomie est certainement une des sciences les plus anciennes, depuis les Babyloniens et les Egyptiens,
étudiée pour des raisons religieuses, pratiques (prévision des saisons pour l'agriculture) et ésotériques
(astrologie). Les Grecs conçoivent le premier modèle de l'Univers, les Arabes continueront leur oeuvre au
Moyen Age. D'autres contrées mal connues à cette époque (Inde, Chine) ou inconnues (en Amérique du Sud)
s'intéressent aussi à l'astronomie.
Au temps des Grandes Découvertes c'est toujours le système géocentrique de Ptolémée
(IIe siècle) qui est reconnu :
la Terre est le centre de l'Univers et les Lune, Mars, Mercure, Jupiter, Vénus, Saturne et le Soleil
(les sept jours de la semaine, d'après les sept planètes connues depuis l'Antiquité) gravitent autour, bien qu'Aristarque de Samos
ait pressenti un modèle héliocentrique au IIIe siècle av. J-C.
La Lune et le Soleil, par leurs mouvements relatifs à la Terre, sont des horloges célestes ; seront élaborés les calendriers lunaires (romain, musulman) et solaires (égyptien, julien puis grégorien actuel). Pour s'accorder avec le Soleil certains calendriers lunaires au début ont évolué en luni-solaires (grec, hébraïque).
Puis viennent les débuts de l'astronomie moderne :
- Copernic (1473 - 1543) : héliocentrisme, qui ne sera accepté que bien plus tard ;
- Kepler (1571 - 1630) : lois sur les orbites planétaires ;
- Galilée (1564 - 1642) : découverte des satellites de Jupiter entre autres travaux (il eut chaud en soutenant la thèse héliocentrique) ;
- Newton (1643 - 1727) : la loi de l'attraction universelle conforte les lois de Kepler ;
- Lalande (1732 - 1807) : élaboration des éphémérides La connaissance des temps ;
- Lagrange (1736 - 1813) : problème des trois corps (Soleil, Terre, Lune) appliqué aux distances lunaires ;
- Laplace (1749 - 1827) : Traité de mécanique céleste, étude des marées, réfraction astronomique ;
- Poincaré (1854 - 1912) : prémices de la théorie de la relativité, cours Les méthodes nouvelles de la mécanique céleste.
5.1.2 Navigation astronomique
Au tout début les astres ne sont que des repères dans le ciel observés par exemple par les Maoris dans le Pacifique. La première méthode de navigation astronomique est celle à hauteur constante de l'étoile Polaire, càd approximativement à latitude constante.
Puis les navigateurs ibériques déduisent la latitude de la hauteur mesurée. L'étoile Polaire n'est pas parfaitement au Nord, elle décrit un cercle de rayon variant au cours des siècles (précession des équinoxes : 3° 30' au XVe siècle, 1° aujourd'hui). La correction à apporter est fonction de la position des "gardes", deux autres étoiles de la constellation, Kochab et Pherkab : Règlement du Nord ; les Arabes procèdent de même dans l'océan Indien. Une autre méthode est utilisée dans l'hémisphère sud : Règlement du Sud (Croix du Sud). La latitude est aussi déterminée à l'aide du Soleil et de tables de sa déclinaison : la méridienne.
Le problème de la latitude est résolu simplement. Il n'en est pas de même pour la longitude qui exige une connaissance précise du temps. Les montres d'alors, plutôt rares, ne sont pas fidèles ; l'heure du bord est déterminée par le midi du Soleil ou la position des gardes (nocturlabe) la nuit et conservée par des sabliers. Plusieurs méthodes ont été envisagées ou utilisées :
- par l'estime, connaissant la différence de latitude et le cap suivi on déduit le changement en longitude (§ 2.1.1, loxodromie) : Règlement des lieues ; si le calcul est mathématiquement exact l'incertitude sur les données explique les erreurs grossières sur les longitudes (et les îles fantômes) mentionnées par les navigateurs d'alors ;
- par rapport aux changements de déclinaison magnétique, sans succès ;
- à l'aide de phénomènes tel que des éclipses, la longitude est déduite de la différence des heures locales d'observation du méridien d'origine et du navire, ce n'est pas tous les jours ;
- suivant les satellites de Jupiter (Galilée), irréaliste en mer ;
- par les distances lunaires (deuxième moitié du XVIIIe) : des tables donnent l'heure à Greenwich en fonction de l'angle entre Lune et Soleil ou étoiles (Jean-Baptiste d'Après de Mannevillette en France, Nevil Maskelyne en Angleterre) ;
- enfin l'invention du chronomètre de marine résolut le problème fin XVIIIe siècle. Les deux méthodes, distances lunaires et chronométrique coexistèrent quelque temps et furent même utilisées conjointement, l'une corroborant l'autre.
5.1.3 Instruments
Les premiers instruments de mesure de hauteur sont rudimentaires : quadrant, astrolabe de mer (version simplifiée de l'astrolabe astronomique) aux XV - XVIe siècles, puis arbalète (bâton de Jacob) et quartier de Davis aux XVI - XVIIe.
Basé sur le principe de la double réflexion (Newton) le premier instrument précis est construit : l'octant (Hadley, 1731), ainsi nommé car constitué d'un limbe de 45°, perfectionné avec un vernier. Il permet de mesurer des angles jusqu'à 90°. Il sera remplacé par le sextant (Campbell, 1757), le limbe couvre 60° pour mesurer des angles jusqu'à 120° (nécessaire pour les distances lunaires). Ils sont construits à l'origine en ébène et ivoire puis en laiton ou alliage léger. L'ajout de filtres, d'une lunette de visée et le remplacement du vernier par un tambour micrométrique vers 1926 donneront la version actuelle de l'instrument.
Le problème de la longitude était critique, bien des catastrophes furent causées par des estimes incertaines.
Sa détermination nécessite de connaître l'heure, soit par la méthode des distances lunaires, longue et
fastidieuse, soit par une horloge fiable.
Le premier chronomètre de marine, un garde temps dont la dérive reste acceptable lors des voyages au
long cours, fut construit par John Harrison (Angleterre), deuxième moitié du XVIIIe. D'autres horlogers
suivirent : Kendall en Angleterre, Le Roy, Berthoud, Bréguet en France. L'horlogerie a progressé depuis
des montres mécaniques à celles à quartz, contrôlées par radiodiffusion de tops horaires.
Il faut noter que les méthodes des distances lunaires et chronométrique étaient pressenties dès le XVIe, mais ne furent utilisables que grâce au développement d'une part d'instruments et d'éphémérides (§ 5.2.3) et d'autre part d'outils mathématiques pour les calculs, trois siècles plus tard.
5.2 Eléments
5.2.1 Mesure de la hauteur d'un astre
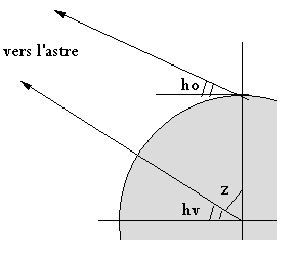
La hauteur d'un astre est le complément de sa distance zénithale z par rapport à l'observateur, aux corrections près (en minutes d'angle) de la mesure au sextant :
- excentricité : erreur par construction du sextant et collimation : décalage du zéro ;
- dépression apparente de l'horizon suivant la hauteur de l'observateur (§ 3.3.2) ;
- réfraction atmosphérique, l'astre est vu plus haut qu'en réalité (§ 5.7.2) ;
- parallaxe, pour rapporter l'angle au centre de la Terre (§ 5.7.3) ;
- demi-diamètre du Soleil (bord inférieur sur l'horizon).
| corrections | Soleil | Etoiles |
|---|---|---|
| hauteur observée | ho = hi ± excentricité et collimation | ho = hi ± excentricité et collimation |
| hauteur apparente | har = ho - 1,77 h½ | har = ho - 1,77 h½ |
| réfraction (1) | ha = har - 0,97 cotg har | hv = har - 0,97 cotg har |
| parallaxe | hv = ha + 0,15 cos ha | - |
| demi-diamètre (2) | hv = hv + 16 minutes (bord inférieur) | - |
| ou globale (3) | hv = ho + correction globale | hv = ho - correction globale |
(1) d'après la formule de Laplace valable pour ho > 15° (à 10°C et 1013 mbar) ;
(2) correction mensuelle supplémentaire à apporter, la distance Terre - Soleil varie au cours des saisons ;
(3) correction globale donnée par les ouvrages, toujours additive pour le Soleil et
soustractive pour les étoiles.
5.2.2 Systèmes de coordonnées
Plusieurs systèmes de coordonnées sont utilisés en astronomie. Pour la navigation :
- coordonnées horaires, les coordonnées du "pied" de l'astre sur la surface terrestre : déclinaison, sa latitude par rapport à l'équateur (nord positive, sud négative), et angle horaire, sa longitude comptée de 0 au méridien d'origine (Greenwich) à 360° vers l'ouest (autrefois exprimé en temps, d'où le nom ; dans le sens rétrograde, càd inverse du sens trigonométrique) ;
- coordonnées horizontales : hauteur de l'astre et azimut, son relèvement. Les formules de trigonométrie sphérique relient ces deux systèmes.
5.2.3 Formules de trigonométrie sphérique
Pour un triangle sphérique (sur la sphère) d'angles aux sommets A, B, C tangents à la surface et de côtés opposés les arcs de grands cercles a, b, c :
cos a = cos b cos c + sin b sin c cos A (1), formule des cosinus des côtés
| sin A | = | sin B | = | sin C | (2), analogie des sinus |
| sin a | sin b | sin c |
cos A = - cos B cos C + sin B sin C cos a (3), formule des cosinus des angles
sin c cotg b = sin A cotg B + cos A cos c (4), formule des cotangentes
5.2.4 Ephémérides
La Terre tourne sur elle même en 23 h 56 min 4,1 s, jour sidéral par rapport à un point fixe dans l'espace ; comme elle s'est déplacée sur son orbite, le jour solaire, mouvement relatif par rapport au Soleil, est de 24 h en moyenne (vitesse variable car orbite elliptique). L'unité de temps, la seconde, en découlait.
La seconde est maintenant définie par une grandeur physique dans le système international d'unités (SI),
l'échelle correspondante est le temps atomique international (TAI).
Les échelles de temps universel (TU ou UT) sont basées sur une seconde
légèrement plus longue :
- UT1 déduit de la rotation de la Terre, non uniforme ;
- UTC, ou temps universel coordonné diffusé par les
signaux horaires, est une linéarisation d'UT1 avec un écart inférieur à 0,9 seconde. Il diffère d'un nombre
entier de secondes de TAI (34 s au 01/01/2009). Une seconde intercalaire est ajoutée de temps en temps
pour tenir compte du ralentissement de la rotation terrestre (ou retranchée, mais cela n'a pas encore eu lieu).
L'expression GMT est périmée.
L'heure locale autrefois définie par le midi du lieu (passage du Soleil au méridien) diffère de UTC suivant le fuseau horaire : 1 h pour 15° de longitude. L'heure légale est celle en usage dans les pays : UTC + 1 h en hiver et UTC + 2 h en été en France.
L'axe de rotation de la Terre est incliné de 23° 26' par rapport au plan de l'orbite (précession des équinoxes, varie suivant un cycle de 26 000 ans et nutation, oscillations d'une dizaine de secondes d'angle et de période 18 ans et 7 mois) ; la déclinaison du Soleil varie entre nord (solstice d'été), zéro (équinoxes de printemps et d'automne) et sud (solstice d'hiver).
L'étude du mouvement des astres a permis de prévoir par calcul leur position. Les éphémérides donnent pour chaque jour :
- l'angle horaire AHvo (à Greenwich, méridien d'origine) du Soleil par heure ou à 0 h UTC et sa variation horaire (qui n'est pas exactement 15°, les 24 h sont un jour moyen) ;
- la déclinaison D du Soleil par heure ou à 0 h UTC et sa variation horaire ;
- l'heure UTC de passage du Soleil au méridien de Greenwich (varie d'environ ± 15 min autour de 12 h au cours de l'année, la différence entre 12 h et heure de passage est appelée équation du temps : temps moyen - temps vrai) ;
- l'angle horaire du point vernal AHso au méridien de Greenwich (§ 5.5) par heure ou à 0 h UTC, sa variation horaire (15° 2,46') est fixe.
5.3 Méridienne
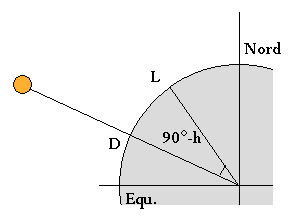
La latitude est calculée à partir de la déclinaison du Soleil (à l'heure UTC de l'observation) et de la distance zénithale, complément de la hauteur vraie, lors de son passage au méridien du lieu (le midi solaire) :
L = D + (90° - hv) Soleil au Sud
L = D - (90° - hv) Soleil au Nord
La hauteur maximale, assimilée à la culmination avec une erreur négligeable La démonstration se trouve dans Traité de navigation, voir la bibliographie. est déterminée par une série de mesures autour de l'heure de passage au méridien local : celle du passage à Greenwich décalée de la longitude estimée (on devrait dire passage au méridien estimé plutôt que méridienne). En toute rigueur il faut corriger les hauteurs du changement de latitude pendant la série de mesures, utiliser un canevas de Mercator. L'écart entre heures de passage à Greenwich et au méridien local, converti en angle, donne une longitude approchée (une erreur de 4 secondes de temps se traduit par une minute de G).
Appliquée à l'étoile Polaire la deuxième expression devient L = hv + A + B + C (corrections suivant sa position, données par des tables des éphémérides).
La méridienne est une survivance du temps où latitude et longitude étaient déterminées séparément
(§ 5.4.2, droite de Sumner). Deux méthodes associées,
- hauteur circumméridienne : correction de la hauteur mesurée lorsque l'heure de passage
au méridien est manquée ;
- hauteurs circumzénithales correspondantes : détermination de l'heure de passage au méridien par
mesures de hauteurs de part et d'autre de la culmination
suivant une démarche précise qui prend du temps.
L'alternative simple est le tracé d'une droite de hauteur (§ 5.4.3), le passage au méridien local n'est
qu'un cas particulier où l'angle au pôle est nul (la formule fondamentale du § 5.4.1 se réduit aux expressions
ci-dessus pour P = 0) et la méridienne n'est plutôt qu'une méthode de secours.
5.4 Droite de hauteur du Soleil
5.4.1 Principe
Le lieu géométrique d'où un astre est vu à la même hauteur est un cercle sur le globe
terrestre. Il suffirait donc de tracer ce cercle de centre les coordonnées du Soleil et de
rayon la distance zénithale sur la carte (si son échelle le permet), son relèvement, et obtenir le point.
En réalité la projection géométrique fait que ce n'est plus un cercle sur la carte
mais une courbe (§ 5.6) et le relèvement est bien trop imprécis, il faut procéder
par calcul.
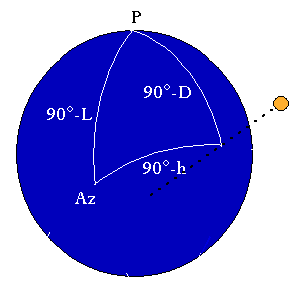
Ce calcul consiste à résoudre le "triangle de position" d'angle au pôle P, écart de longitude entre Soleil et observateur, de côtés adjacents les compléments des latitude et déclinaison du Soleil (des parties de méridien) et de troisième côté la distance zénithale complément de la hauteur hv :
cos (90° - hv) = cos (90° - L) cos (90° - D) + sin (90° - L) sin (90° - D) cos P d'après (1)
L'angle au pôle est P = AHvo - Gouest
ou P = (360° - AHvo) - Gest soit P = - (AHvo + Gest)
c'est l'angle horaire local AHvg
à la longitude g et finalement :
sin hv = sin L sin D + cos L cos D cos AHvg (5)
Il y a deux inconnues, L et G. Pour résoudre l'équation il faut prendre l'hypothèse de l'une ou l'autre connue ou plus ou moins bien estimée : soit la latitude, méthode du parallèle estimé (point de Lalande - Pagel), soit la longitude, méthode du méridien estimé (point de Borda). Enfin, la méthode de Marq de Saint Hilaire, partant d'un point L et G estimées sera la solution ultime.
5.4.2 Droite de Sumner
La longitude est obtenue à partir de la hauteur hv et d'une latitude L connue ou estimée : calcul d'heure,
en sortant cos AHvg de la formule (5) puis G = AHvg - AHvo.
Fin 1837, en mer d'Irlande, le capitaine Sumner (USA) procède ainsi ; faisant le calcul pour des latitudes
différentes il constate que les points obtenus sont alignés. En fait c'est une corde de la courbe de hauteur,
apparaît ainsi la notion de droite de hauteur. Il en déduisit une méthode d'une droite de hauteur déterminée par
calcul à partir de deux latitudes estimées donnant :
- le relèvement vrai de la côte (un heureux hasard fit que la droite tracée passe par le phare de Smalls
sur la côte galloise),
- l'incertitude sur la longitude conséquence de l'erreur sur la latitude,
- l'azimut vrai du Soleil perpendiculaire à la droite de hauteur.
5.4.3 Droite de Marq de Saint Hilaire
La méthode moderne est le point du contre-amiral Marcq de Saint Hilaire dite du vertical estimé (le grand cercle passant par le pied de l'astre et la position estimée), publiée en 1875, en comparant les hauteurs mesurée hv et calculée he à partir d'une position estimée :
he = arcsin (sin L sin D + cos L cos D cos AHvg) (5')
L'azimut du Soleil est calculé par :
| sin Az = | sin AHvg cos D | (6), d'après (2), azimut par l'heure et la hauteur |
| cos he |
L'intercept est la différence entre hv et he (1 minute d'angle = 1 mille). L'azimut est tracé sur la carte à partir du point estimé, sa perpendiculaire située à la distance de l'intercept (point déterminatif), vers le Soleil si hv > he sinon à l'opposé, est la droite de hauteur, tangente à la courbe de hauteur.
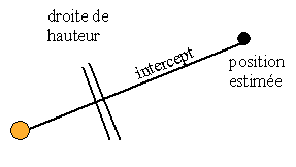
On est situé quelque part sur cette droite de hauteur, le point complet sera déterminé par l'intersection d'une deuxième avec le transport de la première.
Les calculs étaient effectués autrefois à l'aide des logarithmes (tables de Friocourt, 1899), puis de tables spéciales : Perrin (1876) ou Bataille (1911) pour Az, Dieumegard pour he (193?), ou les tables américaines HO249. Elles ont été fort utiles mais sont remplacées maintenant par une simple calculette ou un tableur sur PC.
L'erreur théorique de cette méthode est de moins d'un mille pour des latitudes jusqu'à 60°, hauteur inférieure à 80° (au delà la portion de courbe approchée par une droite est réduite) et un intercept inférieur à 30 milles (pour un écart entre azimuts réel et calculé inférieur au degré).
En pratique restent les erreurs de mesure :
- de hv, une minute se traduit directement par un mille sur l'intercept ;
- du temps qui affecte l'angle au pôle (4 secondes de temps = une minute d'angle), donc he et l'intercept :
Δhe = - cos L sin Az ΔP par dérivation de (5)
et combinaison avec (6).
La grandeur de l'intercept ne préjuge pas de la qualité du point, ces erreurs de mesure ou la position estimée peuvent aussi bien être en cause. Par précaution on refera une mesure et les calculs avec une position estimée éventuellement rectifiée.
5.4.4 Divers
Calcul de l'azimut
| Azimut par la hauteur : cos Az = | sin D - sin he sin L | d'après (1) |
| cos he cos L |
| Azimut par l'heure : tg Az = | sin(-AHvg) | (7), d'après (4) |
| cos L tg D - sin L cos AHvg |
Les tables de Bataille et celles de Perrin sont basées sur l'expression (7).
Versine et haversine
Le sinus verse ou versine est une fonction toujours positive, ce qui permet le calcul par logarithmes :
versine x = 1 - cos x = 2 sin2(x / 2) et haversine x = sin2(x / 2)
Les tables de Dieumegard utilisent les versines, la formule (5) devient :
versine (90° - he) = versine (L - D) + cos L cos D versine (AHvg)
En revenant aux fonctions classiques (un sinus et un produit évités) :
sin he = cos(L - D) + cos L cos D (cos AHvg - 1) (8)
Ces fonctions d'origine britannique sont maintenant abandonnées. Citons aussi la sécante : sec x = 1 / cos x et la cosécante : cosec x = 1 / sin x qui facilitaient les calculs manuels, disparues depuis des tables trigonomériques.
Lever et coucher du Soleil
Les éphémérides indiquent pour différentes latitudes les heures UTC des lever et coucher ainsi que l'azimut : l'écart avec l'heure locale donne une longitude approximative et l'azimut sert à vérifier le compas.
Planètes
Le traitement des hauteurs de Mars, Vénus, Jupiter et Saturne est identique à celle du Soleil (les éphémérides comprennent leurs coordonnées ainsi que celles de la Lune). Le cas de la Lune est plus complexe : étant proche de la Terre la variation de distance suivant son orbite fait que les corrections de demi-diamètre et de parallaxe varient de plusieurs minutes.
5.5 Droite de hauteur des étoiles
5.5.1 Point vernal
De même que pour le Soleil les éphémérides pourraient fournir les déclinaison et angle horaire de chaque étoile. Celles-ci bougeant peu sur la voûte céleste il est plus simple d'indiquer leur position par rapport à un point de référence : le point vernal γ situé sur l'écliptique à l'équinoxe de printemps. Son angle horaire AHso est donné par les éphémérides.
La position de chaque étoile est indiquée bimestriellement par la déclinaison D et l'ascension verse AVa comptée vers l'ouest (sens rétrograde, contraire de l'ascension droite des astronomes ARa), sa distance en longitude du point vernal.
Notations de l'angle horaire AH
- s : du point vernal (temps Sidéral), a : de l'Astre (général), v : du Soleil (temps solaire Vrai),
- o : au méridien d'origine (Greenwich), g : au méridien de l'observateur (à la longitude g).
5.5.2 Droite de hauteur
La même méthode avec les formules (5') et (7) est utilisée, l'angle horaire local est maintenant AHag, AVa est toujours additive :
AHag = AHso + AVa ± G
L'astre n'est visible que lorsque son angle au pôle est inférieur au semi-arc diurne :
cos P = - tg L tg D d'après (5) pour hv = 0
Si D < L - 90° il n'est jamais visible, si D > 90° - L toujours visible (circumpolaire). Dans ces deux cas la formule n'a aucun sens, elle donne un cosinus > 1.
L'observation de deux étoiles ou plus donne un point complet.
5.6 Courbes de hauteur
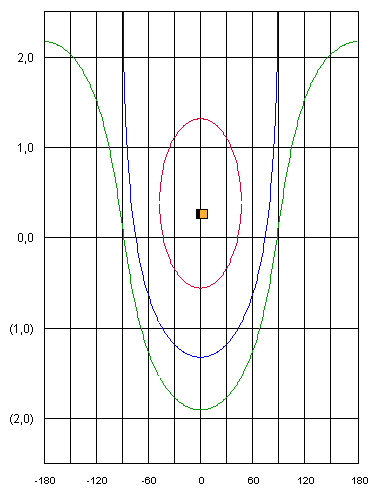
Le cercle de hauteur a pour équation la formule fondamentale (5) ; celle de la
courbe de hauteur Trois manières pour la déterminer :
calculer P suivant L avec (5) puis convertir L en £,
résoudre l'équation du second degré ci-dessous où exp(£) est l'inconnue,
enfin la plus élégante utilise les fonctions hyperboliques
(voir l'ouvrage de Ph. Bourbon dans la bibliographie).
s'obtient en exprimant sin L et cos L en fonction de e£ = tg(L/2 + π/4) :
(e£ + e-£) sin hv = (e£ - e-£) sin D + 2 cos D cos P
La figure représente les courbes pour D de l'astre (en jaune) = 15° N, £ est en radians.
- En rouge, hv = 45° soit en général hv > |D| (valeur absolue de D),
les pôles sont exclus du cercle de hauteur, il est ovalisé verticalement : première espèce.
- L comprise entre D - z et D + z (z : distance zénithale), ici -30 à 60°.
- Sin Pmax = cos hv / cos D et sin L = sin D / sin hv pour Az = 90° et 270°. - En vert, hv = 2° soit hv < |D|, le pôle nord (sud si D était sud)
est inclus, la courbe ressemble à une sinusoïde : deuxième espèce.
- L comprise entre D - z et 180° - (D + z), ici -73 à 77°. - En bleu, hv = 15° soit hv = |D|, le cercle passe par le pôle nord (sud si D était sud),
la courbe est ouverte en parabole : troisième espèce.
- Lmin = D - z, ici -60°, asymptotes à P = ± 90°.
A partir du rayon de courbure local Les démonstrations se trouvent dans l'ouvrage de Ph. Bourbon, voir la bibliographie. : ρ = cos hv / cos P cos D, on calcule l'écart entre courbe et droite de hauteur pour légitimer son approximation.
5.7 Compléments
5.7.1 Orthodromie
Le calcul consiste à résoudre le triangle sphérique dont l'angle au pôle est la différence des longitudes, les côtés adjacents les compléments aux latitudes de départ (1) et d'arrivée (2) et le troisième côté la distance orthodromique m. L'angle initial est A1, de 0 à 180° ou -180° :
cos m = sin L2 sin L1 + cos L2 cos L1 cos(G2 - G1) d'après (1)
| tg A1 = | sin(G2 - G1) | d'après (7) |
| cos L1 tg L2 - sin L1 cos(G2 - G1) |
Les points intermédiaires de la route sont donnés par :
| tg Lx = | sin(Gx - G1) cotg A1 + cos(Gx - G1) sin L1 | d'après (4) |
| cos L1 |
Le point le plus haut en latitude LV, le vertex où l'angle AV est droit, est :
cos LV = cos L1 |sin A1| d'après (2)
cos(GV - G1) = tg L1 / tg LV d'après (4)
Si |A1| < 90° LV est nord sinon sud ; l'écart de longitude par rapport à G1 est du même signe que (G2 - G1). Les points intermédiaires peuvent être calculés par rapport au vertex, mais la formule précédente est préférable, le vertex pouvant être situé à l'extérieur du trajet et donc source de confusion.
La différence de cap au départ ou de relèvement (goniométrie) entre orthodromie et loxodromie est donnée par la correction de Givry : Sa démonstration se trouve dans Traité de navigation, voir la bibliographie.
α = 0,5 (G2 - G1) sin Lm (Lm : latitude moyenne)
5.7.2 Réfraction atmosphérique
La réfraction de la lumière par l'atmosphère relève l'horizon visuel et fait apparaître les astres plus hauts qu'en réalité.
Dépression apparente de l'horizon
On introduit un rayon terrestre fictif (voir § 3.3.2) pour tenir compte de la réfraction atmosphérique.
Deux démonstrations conduisant au même résultat,
- l'une par raisonnement géométrique : R' = R / (1 - 2 γ)
ou R / (1 - K) dans les traités de géodésie,
- l'autre analytique (réfraction des ondes radio) :
R' = R / ( 1 - R / s) avec s : rayon de courbure du trajet lumineux ;
d'où α = (1 - γ) (2 h / R)½ soit 1,77 h½ minutes d'angle pour γ moyen = 0,08 (varie suivant P / T2).
Correction de la hauteur apparente
La formule de Laplace donne la correction pour des distances zénithales z inférieures à 75° (ou des hauteurs supérieures à 15°), au delà son résultat est excessif :
r = α (1 - β) tg z - α (β - α / 2) tg3 z (α et β dépendant des température et pression atmosphérique)
Le premier membre étant prépondérant (le modèle simplifié de la "Terre plate" conduit à cette expression) :
r(z) = 0,97 tg z soit r(har) = -0,97 cotg har minutes d'angle, à 10°C et 1013 mbar.
La formule empirique de Bennett donne directement la correction en minutes pour har exprimée en degrés :
| r(har) = -cotg( har + | 7,31 | ) |
| har + 4,4 |
Pour tenir compte des pression atmosphérique et température appliquer à r les facteurs :
P / 1013 et 283 / (273 + θ)
Les lever et coucher du Soleil sont définis tels que son bord supérieur tangente l'horizon. Son
centre est alors à une hauteur vraie de
- 50 minutes, soit 16' de rayon apparent plus 34' de réfraction.
Les aube et crépuscule sont dûs à la diffraction de la lumière. On distingue les aube et crépuscule
civils : centre du Soleil jusqu'à
- 6°, nautiques : jusqu'à - 12° et astronomiques : jusqu'à - 18°.
5.7.3 Parallaxe
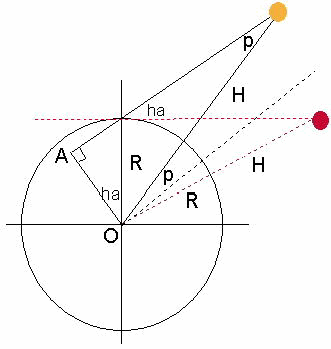
L'angle de parallaxe horizontale π d'un astre situé sur l'horizon géométrique, est
le rayon apparent de la Terre vue de cet astre :
sin π = R / (R + H) (en rouge, R rayon terrestre, H distance).
La correction suivant la hauteur de l'astre est : p = π cos ha ; pour le Soleil :
p = 0,15 cos ha en minute d'angle.
π varie de 0,1 à 0,3' pour Vénus et Mars suivant le mois (leur distance) ; celle de la Lune,
très proche de la Terre, varie de plusieurs minutes autour du degré. La parallaxe est négligeable pour les autres
planètes et les étoiles.
Sur la figure :
sin p = OA / (R + H),
OA = R cos ha,
sin p = R cos ha / (R + H),
p = π cos ha (petits angles),
on voit sur la figure que la parallaxe est toujours additive, hv = ha + p.
5.7.4 Panneaux solaires
A partir de la position géographique connue et des éphémérides les formules (5) et (6) donnent l'orientation et l'inclinaison optimales des panneaux solaires (on néglige les quelques minutes de réfraction et parallaxe).
5.7.5 Satellites artificiels
Les satellites de télévision sont sur une orbite géostationnaire : D est nulle (orbite équatoriale), l'angle au pôle la différence de longitudes entre satellite et observateur et H = 35 786 km. La couverture limite de réception (une courbe de première espèce sur la carte de Mercator) et l'orientation précise des antennes réceptrices sont calculées à l'aide des formules de l'orthodromie.
© G. Navarre, 2006. Màj 16/09/2024.