La rotondité de la Terre est admise depuis les géographes grecs qui utilisaient les coordonnées géographiques latitude L (ou φ) et longitude G (ou λ). Au XVIIIe siècle apparaît la conception de l'ellipsoïde, les dimensions adoptées variant d'un pays à l'autre, puis au XXe le modèle du géoïde, surface équipotentielle du champ de pesanteur terrestre.
L'ellipsoïde de référence est celui du système géodésique WGS 84, de rayon équatorial 6 378,137 km, polaire 6 356,752 km et d'aplatissement 1 / 298,257. La longueur d'un arc d'une minute de latitude varie de 1 843 à 1 862 mètres de l'équateur aux pôles. Mais on considérera la Terre sphérique dans tous les calculs de navigation, le mille nautique a la valeur moyenne de 1 852 mètres.
Une sphère ne peut être représentée à plat en conservant toutes ses caractéristiques. Plusieurs systèmes de projection ont été élaborés dès l'Antiquité, mais la projection conforme, càd conservant les angles, est la seule intéressante pour la navigation puisqu'on utilise les directions. Le géographe flamand Gerhard Kremer dit Mercator crée la projection ainsi nommée et publie une carte du Monde en 1569. Ce système cartographique est utilisé depuis par tous les marins.
Les premiers documents nautiques, les portulans, étaient des descriptions d'itinéraires plutôt que des représentations géographiques d'un monde très mal connu d'ailleurs. Puis vinrent les cartes dites plates-carrées, càd sans projection mathématique : des roses des vents reliées par des marteloires indiquaient les caps des routes principales. Ce principe était suffisant pour des régions limitées comme la Méditerranée.
2.1 Cartes marines
2.1.1 Projection de Mercator
Principe :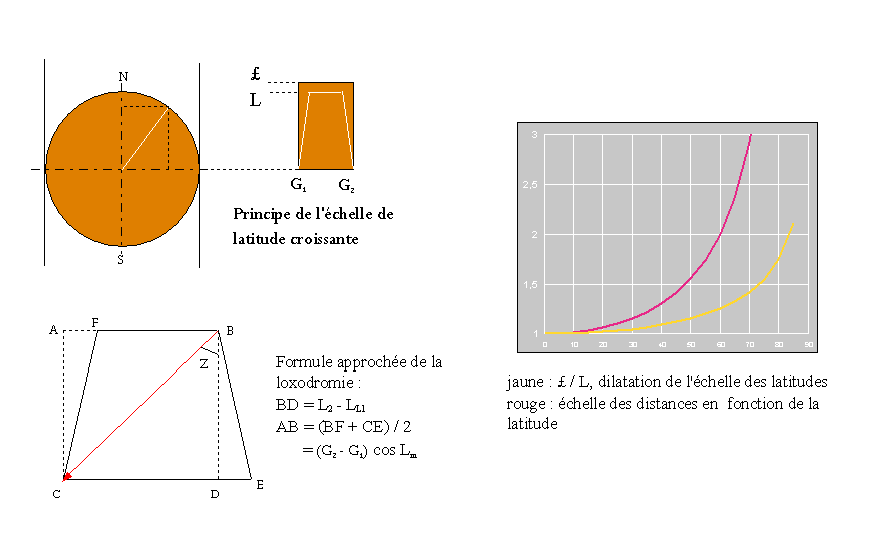
projection cylindrique conforme du globe suivant l'équateur.
Les méridiens et les parallèles, perpendiculaires aux premiers, sont des droites. Les méridiens ne
concourent pas vers le pôle mais restent équidistants, l'échelle en longitude
est dilatée d'un facteur 1 / cos L en s'éloignant de l'équateur.
Pour conserver les angles il faut une échelle en latitude croissante £, telle que :
d£ =
dL / cos L
d'où £ = Ln [tg (
L / 2
+ π /
4)]
Mercator avait construit sa projection par sommation discrète assez rudimentaire ; E. Wright la corrigera en utilisant un pas plus fin. Mais il faudra attendre l'invention des logarithmes et du calcul intégral pour établir l'expression ci-dessus, un siècle plus tard.
La projection tient compte de l'ellipsoïde, un terme correctif est ajouté à l'expression de £ (e : excentricité, § 2.4.1), latitude isométrique :
£ = Ln [tg (
L / 2
+ π / 4
)] + e / 2
Ln [1 - e sin L
/ 1 + e sin L]
Elle est limitée à 80° de latitude, la déformation étant trop importante au delà. Les directions sont obtenues directement sur la carte mais les distances doivent être mesurées par report sur l'échelle des latitudes.
Orthodromie :
La route la plus courte entre deux points sur le globe, un arc de grand cercle de centre celui de la sphère, est représentée par une courbe sur une carte de Mercator, convexe vers le nord dans l'hémisphère nord, inversement dans le sud. Les trajets nord - sud restent des droites, les méridiens sont des grands cercles ainsi que l'équateur. Les calculs de cap, variable, et de distance utilisent les formules de trigonométrie sphérique (§ 5.7.1).
Loxodromie :
Angle de route constant, en ligne droite sur la carte, la distance est supérieure à l'orthodromie (sensible seulement pour les grandes traversées). L'angle de route Rf et la distance m entre deux points sont (la fonction atan2 retourne de -180 à +180°, si < 0 il suffit d'ajouter 360°) :
tg Rf =
G2 - G1 /
£2 - £1
dm = dL /
cos Rf
donc m = L2 - L1
/ cos Rf
A latitude constante on calcule le chemin est-ouest : e = (G2 - G1) cos L.
Ou suivant l'approximation, avec Lm = latitude moyenne (la distance est calculée par la formule précédente ou bien par Pythagore ci-dessous) :
tg Rf =
(G2 - G1) cos Lm /
L2 - L1
m2 = (G2 - G1)2 cos2Lm +
(L2 - L1)2
L'écart avec le calcul exact est fonction de la différence des latitudes et de la distance, mais est négligeable pour des distances jusqu'à 600 milles ou même plus. La limite de 375 milles (voir Guide du navigateur dans la bibliographie) parfois citée pour cette approximation assure en théorie, car dépendant de l'exactitude des cap et loch, une erreur de moins d'une minute sur G déterminée par l'estime :
G2 - G1 =
m sin Rf /
cos Lm
2.1.2 Canevas de Mercator
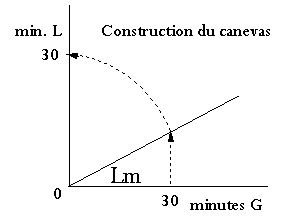
Méthode graphique de construction d'un quadrillage Mercator sur une plage de moins d'un degré autour de Lm. Permet un zoom local sur une partie de carte, d'éviter de tracer directement sur celle-ci...
2.1.3 Autres projections
- Oblique :
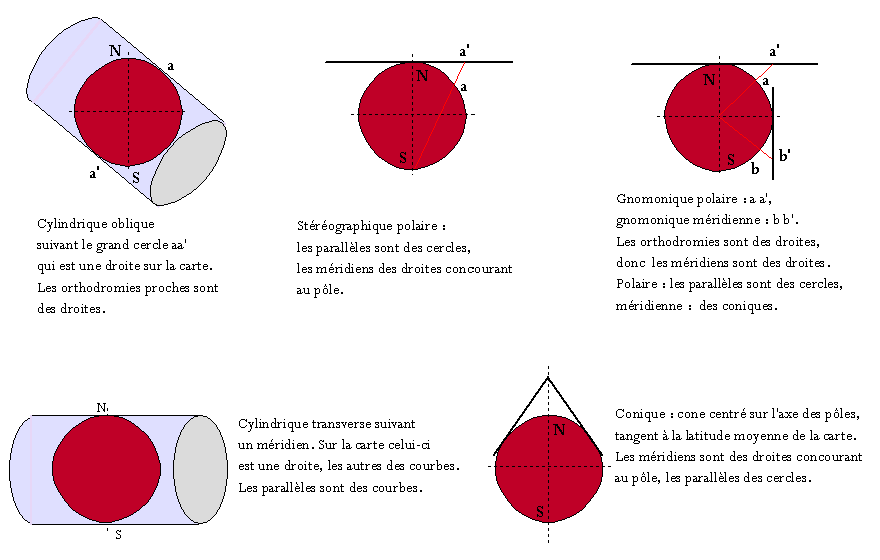projection cylindrique conforme suivant un grand cercle qui sera une droite sur la carte, donc une orthodromie ;
les routes proches seront assimilées à des orthodromies. Utilisée pour les traversées océaniques, par exemple la
carte de l'Atlantique nord 6561 du
SHOM dite "Route du rhum". - Stéréographique polaire : projection azimutale conforme des régions polaires.
- Gnomonique : projection azimutale non conforme, polaire ou méridienne (SH britannique et américain) ; les orthodromies sont des droites, donc tracées aisément, les points sont reportés ensuite sur une représentation conforme pour relever les caps.
- UTM : projection cylindrique conforme suivant un méridien ; représentation mondiale par fuseaux larges de 6° de longitude.
- Lambert : projection conique conforme utilisée pour les cartes terrestres françaises.
- Cylindrique équidistante (plate-carrée) : présente une fausse allure
de projection de Mercator mais l'ordonnée est simplement L. Un exemple est le planisphère
de la NASA par assemblage d'images
satellite.
2.2 Lecture des cartes
Cartouche, caractéristiques et conventions essentielles de la carte, à lire attentivement :
- numéro, titre et référence de l'édition (les corrections postérieures sont indiquées en bas à droite des cartes du SHOM par l'année et le numéro de l'avis), type de projection,
- système géodésique de référence et corrections à apporter aux positions GPS si différent de WGS 84,
- échelle pour la latitude moyenne ou à une L précisée,
- référence du niveau zéro des mers (plus basse mer connue en France),
- référence des altitudes (niveau moyen des mers en France),
- origine des données hydrographiques,
- relèvements exprimés en cap vrai ou magnétique (cartes anglo-saxonnes pour la plaisance),
complété par :
- des roses de compas avec indication de la déclinaison magnétique et sa variation annuelle,
- des tableaux de hauteurs d'eau et courants de marée...
Principales informations :
- contour et physionomie de la côte, amers,
- lignes de sonde, nature des fonds, dangers,
- balisage et feux (hauteur donnée par rapport à une PM de coefficient 95),
- secteurs des feux, alignements d'accès,
- zones diverses (interdites, de mouillage), chenaux de séparation de trafic (Bretagne, Galice).
Les représentations, symboles et abréviations sont définis par une norme internationale (ouvrage 1D du SHOM).
2.3 Documents nautiques
2.3.1 Documents
Ensemble des documents nécessaires (et réglementaires, division 240, avril 2008) :
- un jeu de cartes, de préférence du SHOM,
- des instructions nautiques (hors règlement !) qui complètent les cartes par des descriptions, des vues de paysages et de ports (les photographies aériennes obliques sont les plus instructives), des renseignements et conseils,
- un répertoire des feux (§ 1.4.2),
- un annuaire des marées (sauf Méditerranée),
- le livre de bord où sont notées entre autres les données pour la tenue de l'estime,
- le Règlement international pour prévenir les abordages en mer (RIPAM) ;
et éventuellement un atlas de courants (§ 1.3.3), un répertoire des radiophares (goniométrie)...
2.3.2 Tenue à jour
L'ensemble de la documentation nautique évolue du fait des changements du milieu, meilleure précision des relevés récents, réglementation... Un document non actualisé est dangereux, on veillera à utiliser sa dernière édition complétée par les corrections postérieures. Les corrections à apporter aux documents du SHOM et d'autres informations sont diffusées par les :
- avertissements urgents de navigation (AVURNAV) et
- avis aux navigateurs (AVINAV), rassemblés dans les groupes hebdomadaires d'avis aux navigateurs (GAN) ;
- fascicules de correction des différents ouvrages.
Important : se méfier de tout document ancien, carte, livre... qui ont certainement un intérêt historique mais dont le contenu est périmé.
2.4 Ellipsoïde et géoïde
Dans un système géodésique on utilise l'ellipsoïde avec ses paramètres pour les calculs de L et G, le géoïde comme référence pour l'altitude (en WGS 84 la différence de hauteur entre les deux varie d'environ plus ou moins cent mètres) et pour le calcul de la position en coordonnées cartésiennes géocentriques.
2.4.1 Latitudes
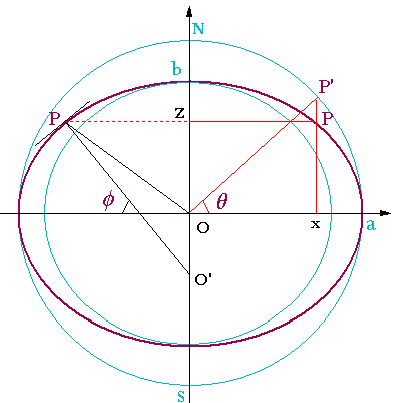
Soit un point P sur le méridien, l'angle entre l'axe horizontal et :
- OP (à gauche) est la latitude géocentrique utilisée dans l'approximation d'une Terre sphérique ;
- O'P (à gauche) normale à la tangente en P à l'ellipse est la latitude géodésique ou géographique φ ; O'P est le rayon normal Rn ou grand rayon (désigné aussi N) ;
- OP' (à droite) est la latitude paramétrique θ qui définit les coordonnées cartésiennes de P suivant (a : rayon équatorial, b : polaire) x = a cos θ et z = b sin θ. Le rayon de courbure du méridien (désigné aussi M) est :
Rm =
(a2 sin2θ + b2 cos2θ)3/2
/ a b
et le rayon d'un cercle parallèle : Rp = a cos θ.
On démontre que tg φ = -dx / dz = (a / b) tg θ. A l'aide de cette relation et du carré de l'excentricité e2 = 1 - (b / a)2, les expressions précédentes deviennent :
Rm =
a (1 - e2) /
(1 - e2 sin2φ)3/2
Rn =
a /
(1 - e2 sin2φ)1/2
Rp = Rn cos φ
D'où les longueurs en mètres des minutes d'arc de latitude et longitude sur l'ellipsoïde WGS 84 :
| Latitude φ | Rm | minute L | Rn | minute G | R local |
|---|---|---|---|---|---|
| 0° | 6 335 439 | 1 843 | 6 378 137 | 1 855 | 6 356 752 |
| 15° | 6 339 703 | 1 844 | 6 379 568 | 1 793 | 6 359 604 |
| 30° | 6 351 377 | 1 848 | 6 383 481 | 1 608 | 6 367 409 |
| 45° | 6 367 382 | 1 852 | 6 388 838 | 1 314 | 6 378 101 |
| 60° | 6 383 454 | 1 857 | 6 394 209 | 930 | 6 388 829 |
| 75° | 6 395 262 | 1 860 | 6 398 150 | 482 | 6 396 706 |
| 90° | 6 399 594 | 1 862 | 6 399 594 | 0 | 6 399 594 |
Le rayon moyen pour l'approximation d'une Terre sphérique est 6 371 km.
Ou on considèrera des sphères locales de rayon
Rl = (Rm Rn)1/2
(rayon de Gauss) à leur latitude moyenne.
La tangente de la latitude géocentrique étant (b / a)2 tg φ, la différence avec φ
atteint -11,5 minutes à la latitude de 45°.
2.4.2 Altitudes
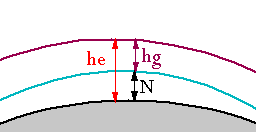
L'altitude he d'un lieu au dessus de l'ellipsoïde se décompose en hg, altitude sur
le géoïde et N, hauteur du géoïde sur l'ellipsoïde appelée ondulation
(peut être négative, en moyenne 48 mètres en France).
Le GPS affiche hg et fournit hg et N dans un message NMEA (§ 7.6).
La surface du géoïde est considérée correspondre au niveau moyen des mers... mais la référence des
niveaux est complexe, se reporter au site de l'IGN.
On prend en compte cette altitude pour passer des coordonnées géographiques à cartésiennes :
x = (Rn + he) cos φ cos λ y = (Rn + he) cos φ sin λ z = [Rn (1 - e2) + he] sin φ
Et inversement, pour retrouver les G, L et he (la fonction atan2 donnera directement la longitude est ou ouest) :
λ = arctg (
y /
x )
φ = arctg ( z /
d ) avec
d = (x2 + y2)1/2
puis
Rn = a /
(1 - e2 sin2φ)1/2
et φ = arctg (
z + Rn e2 sin φ /
d) en trois itérations
he = d /
cos φ - Rn
Le passage d'un système géodésique à l'autre s'effectue par l'intermédiaire des coordonnées cartésiennes
auxquelles on applique une correction de translation des trois axes plus éventuellement une correction
de rotation de chacun et un facteur d'échelle (voir le site de l'IGN).
Ceci explique qu'il faut utiliser des cartes établies dans le même système que celui affiché par le GPS,
ou du moins appliquer les corrections indiquées, loin d'être négligeables (anciennes cartes du SHOM en
ED 50).
2.4.3 Surfaces
Des applications sur PC et certains GPS calculent les périmètre et aire d'un contour fermé à partir des coordonnées géographiques de ses arêtes. Trois méthodes relativement simples donnant d'excellents résultats :
1) A partir du carroyage métrique Lambert (France) ou UTM (Monde), donnant les coordonnées cartésiennes
x et y des n arêtes, les calculs se réduisent à de la géométrie plane :
- les distances entre points par le théorème de Pythagore,
- l'aire du polygone par la formule de l'arpenteur :
S = 0,5 Σ (xi yj - xj yi) avec
i de 0 à n-1 et j = i+1.
Les distances et surface sont celles projetées sur l'ellipsoïde, sans tenir compte de l'altitude.
2) Décomposer la surface en triangles dont les coordonnées géographiques des sommets sont
converties en géocentriques x, y, z (§ 2.4.2) :
- les côtés a, b, c sont obtenus par le théorème de Pythagore en trois dimensions,
- l'aire des triangles plans par la formule de Héron : S = [p (p - a) (p - b) (p - c)]1/2
avec p = (a + b + c) / 2.
L'altitude sur l'ellipsoïde de chaque point est prise en compte. Les triangles doivent rester dans
moins de 6° de latitude (< 600 km) d'étendue pour que l'approximation plane reste valable.
3) Décomposer la surface en triangles sur des sphères de rayon local pris à leur
latitude moyenne. Pour chacun :
- les côtés a, b, c exprimés en arcs sont calculés par la formule de l'orthodromie (voir § 5.7.1),
- l'aire des triangles sphériques par la formule de L'Huilier :
Ω = 4 arctg[tg(p /
2 ) + tg(p - a
/ 2 ) + tg(
p - b / 2
) + tg(p - c /
2 )]1/2
avec p = (a + b + c) / 2 puis S = Ω Rl2
L'incertitude sur les distances et aire calculées dépendra de l'exactitude des coordonnées
géographiques relevées. En considérant les mesures de chaque position distribuées suivant une loi
normale (de Laplace Gauss) d'écart-type spos :
- l'écart-type sur la distance entre deux points (différence de positions) est :
sdist2 = 2 spos2 soit
sdist = 1,414 spos
- l'écart-type sur l'aire d'un rectangle de côtés a et b :
saire2 = a2 sdist2
+ b2 sdist2
= sdist2 (a2 + b2)
soit saire
= 1,414 spos (a2 + b2)1/2
Par exemple, la puce GPS SiRF™ Star III est donnée pour 50% (2/3 de s) des mesures
dans un rayon de 2,5 m, donc spos = 2,5 x 3/2 = 3,75 m.
On considère 95% de la population
pour le calcul des incertitudes de mesure, soit 2 écarts-types,
ici 2 spos = 7,5 m.
L'incertitude relative diminue quand les dimensions du terrain augmentent.
© G. Navarre, 2006. Màj 21/04/2023.