3.1 Cap vrai et cap compas
3.1.1 Nord géographique et nord magnétique
Vers 1600 William Gilbert (Angleterre) imagine un aimant à l'intérieur de la Terre, dont le pôle sud est au Nord et inversement. Les lignes de champ magnétique extérieures sont orientées dans le plan vertical suivant l'inclinaison et dans le plan horizontal suivant la déclinaison. Le pôle nord magnétique est éloigné d'environ 800 milles au sud ouest du pôle géographique ; il se déplace au fil du temps.
La déclinaison D (attention, en Anglais : variation) est la différence entre le méridien géographique (Nord vrai) et le Nord magnétique, ouest si l'aiguille du compas est déviée à gauche du méridien, est à droite. Elle varie suivant le lieu et au cours des ans :
- en Bretagne environ 8° W en 1965, environ 1° W aujourd'hui,
- 15° W aux Caraïbes en 2005,
- déclinaison est dans le Pacifique,
- 40° ou plus aux hautes latitudes nord.
Les cartes marines indiquent la déclinaison locale et sa variation annuelle, ainsi que les zones sujettes à des perturbations magnétiques du sol sous-marin (par ex. une grande épave métallique). Les isogones sont les lignes d'égale déclinaison.
3.1.2 Caps
Le compas n'indique pas exactement le cap magnétique à cause des imperfections de construction et surtout des perturbations des masses métalliques du bord. L'écart est sa déviation d, donc le cap magnétique Cm est :
Cm = Cc + d (Cc : cap compas)
Pour passer au cap vrai Cv sur la carte :
Cv = Cm + D ou Cv = Cc + D + d ou Cv = Cc + w (w = D + d : variation du compas).
les déclinaison et déviation est sont comptées positives, ouest négatives ("EST ce plus OU EST ce moins").
Inversement, pour passer d'un cap vrai au cap compas :
Cc = Cv - D - d
3.1.3 Compensation et régulation
D'abord attribuée à l'humeur fantasque de l'aiguille la déclinaison fut comprise au XVIe siècle. Au XIXe apparaît le problème de la déviation avec les constructions métalliques (Flinders : aimants de compensation, Poisson, Kelvin).
Le modèle est basé sur l'action des fers durs, masses métalliques ayant une aimantation permanente, et celle des fers doux dont l'aimantation varie suivant le cap du navire. En décomposant leurs effets en actions longitudinales et transversales (A. Smith, GB) :
d = A + B sin Cc + C cos Cc + D sin 2Cc + E cos 2Cc
Leur correction se fait en plaçant des aimants dans l'habitacle du compas : compensation. La démarche de compensation d'un compas et la démonstration de la formule d'A. Smith sont décrites dans Traité de navigation, voir la bibliographie.
L'inclinaison des lignes de champ (nulle à l'équateur, environ 60° aux latitudes moyennes) agissant sur l'équilibre de la rose du compas, la compensation effectuée n'est valable que pour une zone océanique donnée (à peu près zone A: Atlantique Nord, B: Atlantique Sud et région intertropicale du Pacifique, C: Pacifique Sud). Les compas modernes sont dédiés à une zone par construction.
La déviation résiduelle (< 5°) mesurée par rapport à des directions connues est portée sur une courbe en fonction de Cc : régulation.
Vérification du compas par alignements, azimuts de l'étoile Polaire et des lever et coucher du Soleil, et maintenant par le cap du GPS en l'absence de dérive.
Montage : des points précédents découle l'importance de placer le compas à l'abri de sources de perturbation, d'éviter de déplacer des masses métalliques au voisinage après la compensation et de maintenir la rose horizontale (montage sur cardans).
3.2 Routes
3.2.1 Estime
Les éléments de la route suivie : cap compas Cc, vitesse surface Vs (celle du loch) et heure, doivent être enregistrés périodiquement dans le livre de bord, au moins à chaque quart et systématiquement en cas de changement de cap ou d'allure, afin d'en déduire la position estimée à tout moment.
Le vent entraîne une dérive de quelques degrés, la route suivie n'est pas strictement dans l'axe du navire, surtout pour les voiliers mais un fardage important peut rendre un bateau à moteur sensible. La route surface Rs est le cap vrai corrigé de la dérive (positive tribord, négative bâbord), soit :
Rs = Cc + w + dervent (corriger le cap)
On passe ensuite à la route fond Rf par construction graphique entre vecteur surface (Rs, Vs) et vecteur courant (C, direction et vitesse pour chaque heure). Sur plusieurs heures on utilisera la commutativité de l'addition de vecteurs.
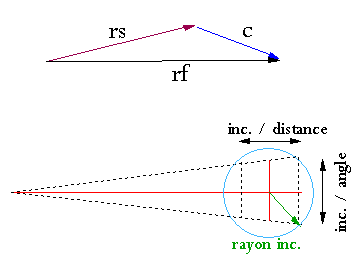
Une incertitude de ± x° sur le cap se retrouve sur Rf et engendre une ouverture pour une distance fond m de : 2 m tg x et ± y % du loch une plage de : 2 m y / 100, déterminant un quadrilatère. Sa demi-diagonale est le rayon du cercle d'incertitude sur la position :
r = m (tg2x + (y/100)2)½
On voit facilement que, quels que soient les changements de cap intervenus, ce rayon ne dépend que de la distance parcourue.
Le courant étant connu avec plus ou moins de précision un autre rayon d'incertitude calculé de façon analogue s'ajoute au premier. La position estimée est donc approximative et doit être régulièrement recalée par un point.
3.2.2 Détermination
La route est tracée, soit directe, soit fragmentée pour parer des obstacles, et les caps et distances mesurés sur la carte.
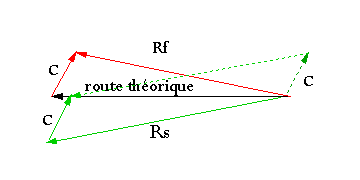
La route surface sera déterminée pour compenser la dérive due au courant. Sur la figure,
- en noir : route théorique à la vitesse Vs,
- en rouge : par addition du vecteur courant C donne la route fond résultante (Rf, Vf),
- en vert : construction pour déterminer la route surface (Rs, Vs) pour compenser ce
courant, la route fond sera celle théorique voulue avec la vitesse fond Vf résultante.
Le cap compas est déterminé par :
Cc = Rs - w - dervent (faire valoir la route)
Le courant variant au cours de la marée cette construction doit être faite heure par heure. Mais dans le cas où une renverse de courant fait que son action est symétrique (par ex. traversée de la Manche en environ 12 heures) la route la plus rapide sera celle sans compensation.
La même construction graphique est utilisée pour définir une route de poursuite.
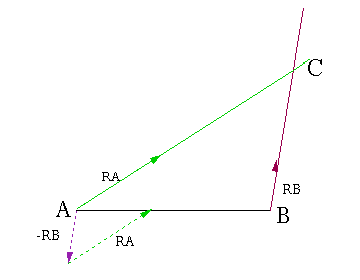
Ci-contre le navire A doit aller à la rencontre de B dont les cap, vitesse et gisement
initial par rapport à A sont connus. On utilise pour la construction un vecteur de route de B
(tirets bruns) en sens inverse, la combinaison avec celui de A donne la vitesse relative
(sur le segment AB) entre les deux bateaux. La rencontre aura lieu en C, au bout d'un temps
dépendant de la distance initiale AB (triangles semblables).
Si A pointait toujours vers B au lieu d'anticiper le déplacement de ce dernier il décrirait un
trajet dit "course du chien".
3.2.3 Allongements de route
| écart de : | allongement |
|---|---|
| 10° | 2 % |
| 20° | 6 % |
| 30° | 15 % |
| 40° | 31 % |
Plusieurs raisons feront s'écarter du cap initial :
progression moins pénible dans une mer formée, pour profiter d'une veine de courant ou
l'éviter, allure plus rapide...
Le tableau indique l'augmentation de distance suivant l'écart de route α :
m' = m / cos α.
C'est aussi le gain de vitesse nécessaire pour conserver au moins le même temps de
parcours (tenir compte du bord de retour sur la route initiale).
3.3 Points
Les méthodes décrites ci-après sont pratiquées en navigation côtière, au large on utilisera le point astronomique et la radionavigation. Le point est obtenu par intersection de directions, distances, lignes de sonde combinées entre elles.
Bien qu'exactes géométriquement elles sont toutes grevées d'une incertitude (précision des mesures).
Ce n'est pas gênant, il suffit d'en tenir compte ; l'important est la réalité
du point, même approximatif, et non pas l'apparence trompeuse d'une position précise.
D'autre part le but d'une carte est d'indiquer les zones d'eau saine, où l'on peut
passer sans problème, et les dangers que l'on doublera au large... et non pas le moindre caillou.
| échelle | distance | carte |
|---|---|---|
| 1 / 7 620 000 | 4 milles | 6561, Atlantique Nord |
| 1 / 1 000 000 | 0,5 mille | 7211, Golfe de Gascogne |
| 1 / 149 000 | 150 mètres | 7345, Guadeloupe |
| 1 / 50 000 | 50 mètres | 7033, Baie de Quiberon |
| 1 / 10 000 | 10 mètres | plans de ports |
Ci-contre quelques distances représentées par un millimètre sur la carte, à comparer avec l'incertitude de position de 10 mètres d'un GPS dans le meilleur des cas.
3.3.1 Directions
a) Alignement : artificiel ou naturel, le moyen le plus simple donnant une position certaine sur sa ligne. Prendre garde à ce que le sommet d'un rocher vu à marée haute corresponde bien à sa base vue à marée basse et qui est celle dessinée sur la carte.
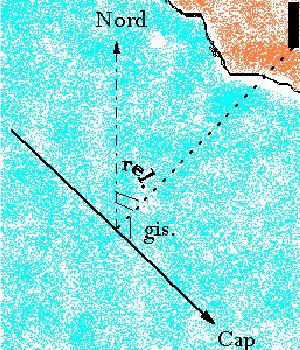
b) Relèvement : angle sous lequel est vu un amer par rapport au Nord, mesuré à l'aide du compas de relèvement, ou mieux mesure à l'aide de taximètres du gisement (angle de 0 à 360° par rapport à l'axe du bateau) et calcul du relèvement compas : Rc = Cc - gis. converti ensuite en relèvement vrai Rv (§ 3.1.2) pour le tracer sur la carte.
L'incertitude sur l'angle mesuré engendre une ouverture d'autant plus grande que l'amer est éloigné (par ex. : 0,1 M par mille pour ± 3°, § 3.2.1). Le point obtenu par deux relèvements croisés sera situé dans un quadrilatère dont la surface croît avec la distance des amers. Assimilé à un parallélogramme on calcule ses diagonales (§ 3.3.5), des axes de l'ellipse d'incertitude qui se rapproche d'un cercle pour des relèvements à angle droit.
Le point par trois relèvements n'améliore pas la précision. D'une part la côte offre rarement trois amers idéalement espacés de 120° et à la même distance ; d'autre part on n'est pas dans le triangle formé par l'intersection des trois droites mais dans le polygone d'incertitude bien plus grand (il suffit de déplacer une droite pour faire apparaître un autre "chapeau"). Si un triangle important indique un point approximatif le contraire n'est pas vrai, c'est peut être un heureux hasard. Le meilleur cas reste deux relèvements à 90°, le troisième servant de contrôle de vraisemblance.
Important : le gisement ou relèvement constant d'un autre bateau indique des routes de collision.
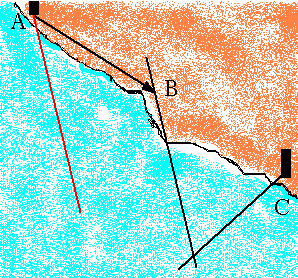
c) Transport d'un relèvement : le relèvement de A est translaté suivant AB, angle de route et distance fond parcourue par le bateau. Le point est obtenu par intersection avec celui de C.
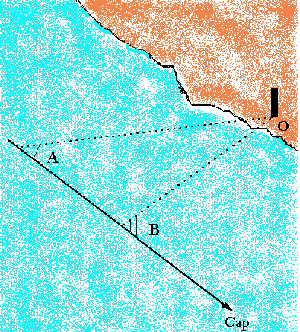
d) Relèvements successifs d'un même amer. A et B sont les gisements, AB la distance parcourue :
OB = AB sin A / sin (B-A)
(table XL de Friocourt) ou détermination par construction graphique. En particulier
OB = AB pour B = 2 A (doublement de l'angle d'étrave).
Les deux gisements pris en avance permettent de se positionner avant de doubler l'amer.
Plus simple que le calcul général ci-dessus : on relève la distance AB lorsque B est à 90° et OB = AB tg A.
Outre l'incertitude des relèvements cette méthode ainsi que la précédente sont tributaires de la précision sur la route parcourue.
3.3.2 Distances
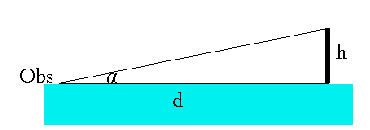
a) En deçà de l'horizon par mesure au sextant de la hauteur d'un amer :
tg α = h / d d'où d = 1,86 h / α
avec d milles, h mètres corrigée de la marée, α minutes d'angle (table XIV de Friocourt).
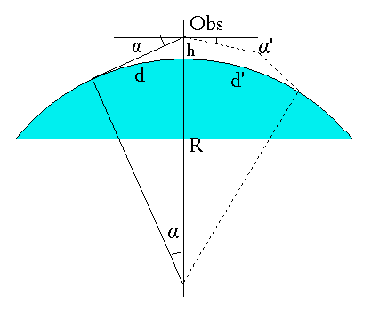
b) Au delà de l'horizon : la distance de l'horizon visuel dépend de la hauteur de l'observateur. En théorie (partie gauche) :
(tg α)2 = ((R + h)2 - R2) / R2
soit α = (2 h / R)½
et darc = (2 h R)½
en négligeant les termes de second ordre et assimilant α à sa tangente. Si h mètres, α minutes et d milles : α et d = 1,93 h½.
En réalité (partie droite) la réfraction de la lumière par l'air relève l'horizon, diminuant α et augmentant d. On considère un rayon terrestre fictif (§ 5.7.2) :
R' = R / (1 - 2 γ) = 1,19 R
pour γmoyen = 0,08 (varie de 0,04 à 0,16), et (table XII de Friocourt) :
α' = 1,77 h½
dépression apparente et
d' = 2,09 h½ distance de l'horizon visuel

Pour un élément de hauteur H émergeant sur l'horizon :
d = 2,09 (h½ + H½)
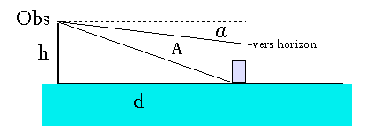
c) En deçà de l'horizon (bis) : la distance d'un sujet est calculée à partir de l'angle A mesuré entre l'horizon et sa flottaison, suivant :
d (mètres) = h / tg(A + α')
(α' = dépression apparente de l'horizon) avec une bonne approximation pour A >= 5 minutes (table XVI de Friocourt, mais la formule utilisée est différente).
Inversement, A + α' est la dépression apparente du pied d'une côte en deçà de l'horizon, à la distance d (table XIII de Friocourt).
3.3.3 Arc capable
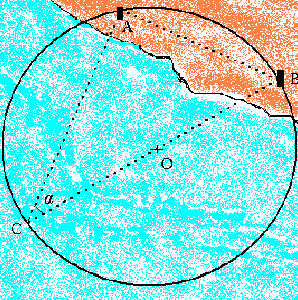
Le lieu géométrique d'où deux amers sont vus sous le même angle mesuré au sextant est un cercle passant par ces deux points.
Soit deux amers A et B vus sous l'angle α : BAC = 90° et ABC =
90° - α, le diamètre du cercle est BC = AB / sin α. A partir de là, deux méthodes
pour déterminer son centre par croisement :
- de deux droites en A et B faisant des angles de 90° - α avec AB ;
- du rayon calculé du cercle (AB / 2 sin α) porté depuis A et B.
La précision de l'angle mesuré au sextant fait que l'erreur sur le diamètre est pratiquement négligeable. Arcs capables et alignements sont les deux méthodes de point considérées certaines.
3.3.4 Lignes de sonde
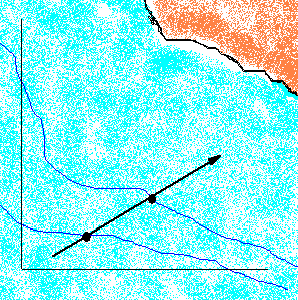
Reconnaissance d'une ligne de sonde corrigée de la marée ou d'une variation de profondeur entre deux.
Intercalaire de sonde : le cap du bateau et la distance parcourue entre deux sondes sont portés sur un calque à la même échelle que la carte. On le déplace sur celle-ci jusqu'à obtenir la coïncidence... Par précaution la position doit être confirmée par un relèvement ou une distance.
Une ligne de sonde remarquable permet de se situer simplement lorsqu'on vient du large, par ex. la ligne des 100 mètres à distance régulière de la côte nord espagnole.
3.3.5 Ellipse et cercle d'incertitude
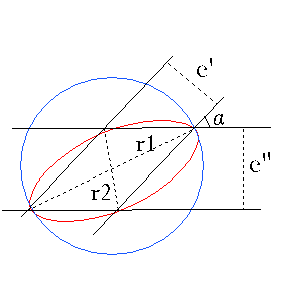
Quelles que soient les lignes de position (droite ou arc de cercle) croisées pour obtenir
un point, on peut assimiler le quadrilatère engendré par l'incertitude sur leur détermination
à un parallélogramme et calculer ses diagonales en fonction des ouverture ou écart en distance e'
et e'' (§ 3.2.1) et de l'angle α entre elles :
r = (e'2 + e''2
± 2 e' e'' cos α)½ / sin α
Pour α droit elles sont égales : r = (e'2 + e''2)½.
Quand l'angle tend vers 0 ou 180° une des diagonales tend vers e' ou e'',
la position devient indéterminée sur l'autre.
Les écarts en longitude et latitude sont obtenus par projection sur les coordonnées. On simplifie en considérant le cercle d'incertitude dont la plus grande diagonale est le diamètre, soit directement les écarts nord-sud et est-ouest, minima pour α droit. Cette simplification par excès va dans le sens de la sécurité et facilite calculs et tracés.
Si les erreurs e' et e" sont connues suivant une distribution statistique (obtenue par un nombre significatif de mesures pour déterminer chaque droite) on peut calculer le rayon du cercle d'erreur probable.
© G. Navarre, 2006. Màj 28/08/2023.